probabilités étranges de non-transitive - Grime dés
Michael de Podesta a fait le calcul sur « Grime Dice » - six cubes côtés dont les côtés moyenner à 3,5, mais dont les valeurs sont face à tous radicalement différents:
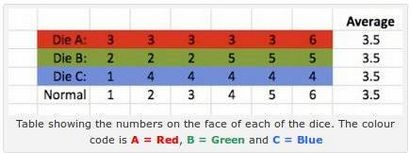
La chose intéressante à propos de ces derniers est que les chances d'un dé battre une autre sont simples à calculer, mais changer radicalement une fois que vous commencez à rouler dés par paire. Il est un beau morceau de mathématiques de probabilité contre-intuitif:
La propriété étonnante de ces dés est perceptible lorsque vous les utilisez compétitifs - à savoir que vous lancez un dé contre un autre. Si vous roulez chacun d'entre eux contre un dé normaux alors que vous pourriez attendre, chaque dé gagneront aussi souvent qu'il va perdre. Mais si vous les rouler les uns contre les autres il arrive quelque chose étonnante.
Le fait que dés A bat B Dice, et bat dés B Dice C ne garantit pas que dés A battra dés C. Wow!
Et que diriez-vous ceci: Si vous doublez 'roll 2 dés A s « s contre 2 Dice B » - les chances changent autour et maintenant le B « s va battre les A « s. Est-ce vraiment possible? Eh bien oui, et juste pour me convaincre que j'ai écrit une feuille de calcul (fichier .xlsx) et Generated les tables en bas de l'article. Si vous le téléchargez, vous pouvez changer les chiffres pour essayer d'autres combinaisons.



preuves zéro connaissance sont l'un des concepts les plus importants dans la cryptographie: ils sont un moyen de « valider un calcul sur les données privées en permettant un démonstrateur de générer une preuve cryptographique qui affirme à l'exactitude de la sortie calculée » - en d'autres termes , un moyen de prouver que quelque chose est vrai sans apprendre les détails.


Le paysage de développement web actuel est truffé de mots à la mode et de la technologie qui obtient presque abandonné dès qu'il est fait. Si vous ne l'avez jamais écrit une ligne de code avant, il peut être difficile de comprendre ce qui vient, ce qui est là pour rester, ou comment obtenir ahead.This Débutant Développement Web Bundle est un excellent endroit [...]