The Dude Math Qu'est-ce qu'un diagramme de Venn
Certaines choses en mathématiques sont allés mainstream. Arithmétique est utilisé par à peu près tout le monde sur une base quotidienne et beaucoup d'autres idées de mathématiques sont utilisées en dehors du monde douillet de la salle de classe, aussi. Par exemple, je l'ai sur la bonne autorité (de ma femme) est fréquemment utilisé le sujet de mathématiques d'aujourd'hui en cours d'anglais du secondaire. Qu'est ce que ça pourrait être? Eh bien, aujourd'hui, nous parlons de diagrammes de Venn.
Comment faire un diagramme de Venn
Pour un diagramme de Venn, commencez par dessiner un rectangle. La zone à l'intérieur de ce rectangle représente toutes les choses possibles contenues dans notre diagramme. Dans notre cas, disons que la zone à l'intérieur de notre rectangle représente l'ensemble de tous les entiers positifs: < 1, 2, 3, 4. >.
L'étape suivante consiste à dessiner des cercles qui se chevauchent à l'intérieur de ce rectangle. La zone à l'intérieur de chacun de ces cercles représente un sous-ensemble des choses dans le grand rectangle. Ainsi, dans cet exemple un cercle représente un sous-ensemble de l'ensemble des nombres entiers positifs. Commençons par dessiner un cercle contenant les nombres entiers positifs qui sont supérieurs à 5 qui est l'ensemble < 6, 7, 8, 9, 10, ... >. Et puis nous allons dessiner un autre cercle (qui chevauche la première) contenant les nombres entiers positifs qui sont moins de 10 qui est l'ensemble < 1, 2, 3, 4, ..., 8, 9 >.
Qu'est-ce que les régions dans Chevauchement diagrammes de Venn Mean?
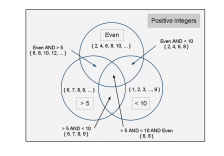
Pourquoi ces cercles doivent se chevaucher? Eh bien, le but d'un diagramme de Venn est de montrer toutes les relations possibles entre les différents ensembles représentés par chacun des cercles. Et, comme nous le verrons dans une minute, toutes ces relations sont décrites par les différentes régions qui se chevauchent. Dans notre cas, les deux cercles représentant des nombres entiers positifs qui sont supérieurs à 5 et des nombres entiers positifs qui sont inférieurs à 10 ont une zone de chevauchement qui représente l'ensemble des nombres entiers positifs qui sont à la fois supérieur à 5 et inférieur à 10, en d'autres termes, la ensemble < 6, 7, 8, 9 >.
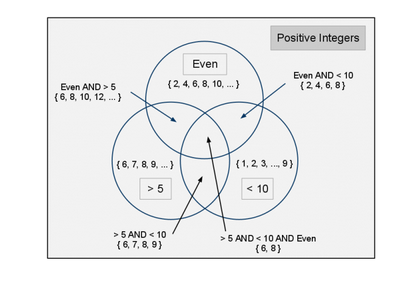
Maintenant, nous allons ajouter un autre cercle à notre diagramme qui représente tous les entiers pairs qui est positif, tous les entiers positifs qui sont divisibles par 2. Ce nouveau cercle doivent se chevaucher chacun des deux précédents que nous avons déjà tiré. Si vous dessinez, vous verrez qu'il ya un total de sept régions dans les cercles de ce diagramme de Venn: Trois représentant les grands ensembles contenus dans les cercles d'origine; trois représentant les diverses combinaisons de paires de ces ensembles: qui est la fois plus de 5 et moins de 10 région, le temps supérieur à 5 et même région, et le même temps inférieur à 10 et même région; et, last but not least, il y a une région au centre de notre diagramme de Venn représentant des nombres entiers positifs qui sont à la fois supérieur à 5, à moins de 10, et même, qui est la paire de numéros < 6, 8 >.
Qu'est-ce que peut représenter le diagramme de Venn?
Nombre de la semaine
Avant de terminer en place, il est temps pour le numéro vedette de cette semaine choisie parmi les différents numéros du jour affiché sur la page Facebook du Math Mec. Le numéro de cette semaine est de 10,7. Qu'est-ce que c'est? Il est la hauteur du mont Everest-la plus haute montagne sur Terre écrit en termes de la hauteur du plus haut bâtiment sur Terre 160 étages (2717 pieds) Burj Khalifa à Dubaï. Si vous empilez 11 de ces bâtiments l'un sur l'autre, ils avaient atteint le sommet du mont Everest. Imaginez monter ces escaliers!
Comment at-Trick Numéro de la semaine dernière marche?
Une dernière chose: Avez-vous savoir comment le deuxième numéro astuce que nous avons parlé de travaux la semaine dernière?
L'astuce a quelque chose comme ceci: Pensez à un nombre compris entre 1 et 10. Maintenant, doubler ce nombre et ajoutez 10 au résultat. Ensuite, diviser ce nouveau numéro par 2, puis soustrayez votre numéro d'origine. Quand vous faites cela, vous aurez toujours 5. Mais pourquoi?